Advanced Engineering Mathematics, 7th Edition

19.4 Zeros and Poles

INTRODUCTION

Suppose that z = z₀ is an isolated singularity of a function f and that

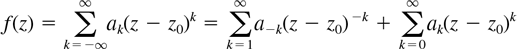(1)

is the Laurent series representation of f valid for the punctured open disk 0 < |z − z₀| < R. We saw in the preceding section that a Laurent series (1) consists of two parts. That part of the series in (1) with negative powers of z − z₀, namely,

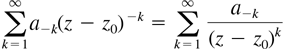(2)

is the principal part of the series. In the discussion that follows we will assign different names to the isolated singularity z = z₀ according to the number of terms in the principal part. ...