19.5 Residue Theorem
INTRODUCTION
We saw in the last section that if the complex function f has an isolated singularity at the point z0, then f has a Laurent series representation
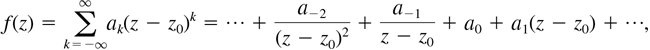
which converges for all z near z0. More precisely, the representation is valid in some deleted neighborhood of z0, or punctured open disk, 0 < |z − z0| < R. In this section our entire focus will be on the coefficient a−1 and its importance in the evaluation of contour integrals.
 Residue
Residue
The coefficient a−1 of 1/(z − z0) in the Laurent series given above is called ...
Get Advanced Engineering Mathematics, 7th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

