In Chapter 17 we emphasized the algebraic definitions and properties of complex functions. In order to give a geometric interpretation of a complex function w = f(z), we place a z-plane and a w-plane side by side and imagine that a point z = x + iy in the domain of the definition of f has mapped (or transformed) to the point w = f(z) in the second plane. Thus the complex function w = f(z) = u(x, y) + iv(x, y) may be considered as the planar transformation
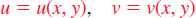
and w = f(z) is called the image of z under f.
FIGURE 20.1.1 indicates the images of a finite number of complex numbers in the region R. More ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month, and much more.
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.
Julian F.
Head of Cybersecurity
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.
Addison B.
Field Engineer
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.
Amir M.
Data Platform Tech Lead
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.
