Advanced Equity Derivatives: Volatility and Correlation

Chapter 4Local Volatility and Beyond

The local volatility model was independently developed in the early 1990s by Derman and Kani and by Dupire. It has arguably become the benchmark model to price and hedge a wide range of equity exotics such as digitals, Asians, and barriers, but fails on certain payoffs such as forward start options, which are better approached using a stochastic volatility model. The model can be difficult to implement since it requires a high-quality, smooth implied volatility surface as input, and simulation of all intermediate spot prices until maturity using short time steps.

4.1 Local Volatility Trees

The local volatility model is best visualized on a binomial tree: instead of using the same volatility parameter to generate the tree of future spot prices (Figure 4.1) the local volatility model uses a different volatility parameter at every node (Figure 4.2). The option is then priced as usual using backward induction.

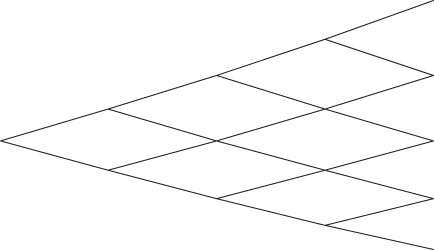
Figure 4.1 Binomial tree with constant volatility.

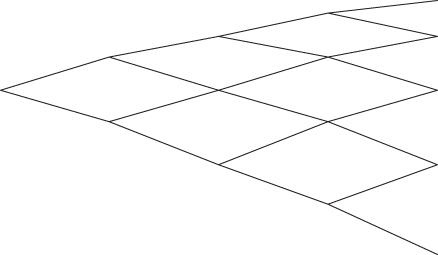
Figure 4.2 Binomial tree with local volatility.

Given a local volatility function σ_loc(t,S) it is relatively easy to construct a tree and then compute the corresponding model-implied volatilities σ^*(K, T). A step-by-step guide can be found in Derman and Kani (1994).

In practice we ...