CHAPTER 5
LINEAR LEAST-SQUARES ESTIMATION: SOLUTION TECHNIQUES
This chapter discusses numerical methods for solving least-squares problems, sensitivity to numerical errors, and practical implementation issues. These topics necessarily involve discussions of matrix inversion methods (Gauss-Jordan elimination, Cholesky factorization), orthogonal transformations, and iterative refinement of solutions. The orthogonalization methods (Givens rotations, Householder transformations, and Gram-Schmidt orthogonalization) are used in the QR and Singular Value Decomposition (SVD) methods for computing least-squares solutions. The concepts of observability, numerical conditioning, and pseudo-inverses are also discussed. Examples demonstrate numerical accuracy and computational speed issues.
5.1 MATRIX NORMS, CONDITION NUMBER, OBSERVABILITY, AND THE PSEUDO-INVERSE
Prior to addressing least-squares solution methods, we review four matrix-vector properties that are useful when evaluating and comparing solutions.
5.1.1 Vector-Matrix Norms
The first is property of interest is the norm of a vector or matrix. Norms such as root-sum-squared, maximum value, and average absolute value are often used when discussing scalar variables. Similar concepts apply to vectors. The Hölder p-norms for vectors are defined as
(5.1-1)
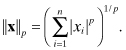
The most important of these p-norms are
(5.1-2)
(5.1-3)
(5.1-4)
The l2-norm

