Advanced Numerical and Semi-Analytical Methods for Differential Equations

1Basic Numerical Methods

1.1 Introduction

Differentialequations form the backbone of various science and engineering problems viz. structural mechanics, image processing, control theory, stationary analysis of circuits, etc. Generally, engineering problems are modeled in terms of mathematical functions or using relationships between the function and its derivatives. For instance, in structural mechanics the governing equation of motion

(1.1)

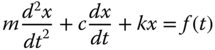
associated with Figure 1.1 is expressed in the form of differential equation with respect to the rate of change in time.

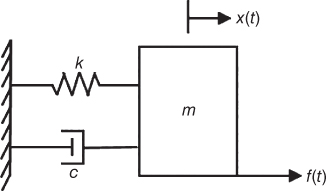
Figure 1.1 Mechanical system.

Here m, c, and k are mass, damping, stiffness parameters, respectively, and f(t) is the external force applied on the mechanical system.

There exist various techniques for solving simple differential equations analytically. Modeling of differential equations to compute exact solutions may be found in Refs. [1–3]. But, due to complexity of problems in nature, the existing differential equations are rather cumbersome or complex (nonlinear) in nature. Generally, computation of exact or analytical solutions is quite difficult and in such cases, numerical methods [4–8] and semi‐analytical methods [9] are proved to be better. In this regard, the numerical and semi‐analytic techniques comprising series ...