Finite element method (FEM) has wide applications in various science and engineering fields viz. structural mechanics, biomechanics and electromagnetic field problems, etc. of which exact solutions may not be determined. The FEM serves as a numerical discretization approach that converts differential equations into algebraic equations. In this regard, the weighted residual methods discussed in Chapter 3 convert governing differential equation to a system of algebraic equations over the entire domain Ω, whereas FEM is applied to finitely discretized elements of the global domain Ω. Also, the finite difference technique discussed in Chapter 5 generally considers the spacing of nodes such that the entire domain is partitioned in terms of squares and rectangles. The FEM overcomes this drawback as depicted in Figure 6.1 by spacing the nodes such that the entire domain is partitioned using any shape in general.
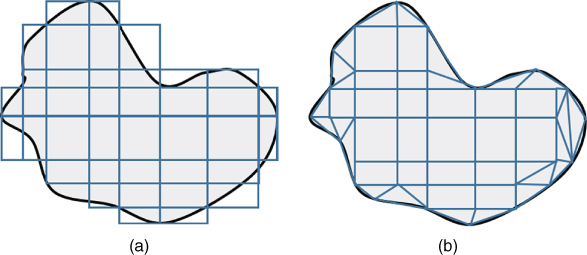
Figure 6.1 (a) Finite difference and (b) finite element discretization of arbitrary object.
Figure 6.2 Nodal points for the domain Ω = [a, b].
In this chapter simple differential equations are solved in order to have better understanding of the finite element technique. There exist various standard books [1–7] and the references mentioned ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month, and much more.
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.
Julian F.
Head of Cybersecurity
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.
Addison B.
Field Engineer
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.
Amir M.
Data Platform Tech Lead
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.
