Advances in Heavy Tailed Risk Modeling: A Handbook of Operational Risk

CHAPTERSEVEN

Single Risk Closed-Form Approximations of Asymptotic Tail Behaviour

In Chapter 6, a set of special sub-families of annual loss loss distribution approach (LDA) models were developed which admitted closed-form exact representations. That is, closed-form representations were obtained for the distribution of the annual loss Z = X₁ + · · · + X_N represented by a compound process model with LDA structure in which the frequency is N ~ Poisson(λ) and the severities are independent and identically distributed (i.i.d.) X_i(t) ~ F_X(x), and N and X_i are independent. The exact distribution of the annual loss processes can be expressed analytically as a mixture distribution comprised convolved distributional components with Poisson mixing weights for N > 0,

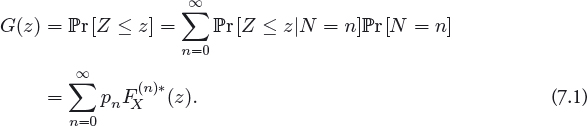
Here, = r[X₁ + X₂ + · · · + X_n ≤ z] is the n-th convolution of the severity distribution F_X(·) calculated recursively as

with = 1 if z ≥ 0 and zero otherwise. Note, throughout this chapter we refer to F as the distribution for the severity, ...