Algebra and Trigonometry, 5th Edition

Chapter 6 Summary and Review

Study Guide

KEY TERMS AND CONCEPTS	EXAMPLES
SECTION 6.1: TRIGONOMETRIC FUNCTIONS OF ACUTE ANGLES
Trigonometric Function Values of an Acute Angle $\theta$ Let $\theta$ be an acute angle of a right triangle. The six trigonometric functions of $\theta$ are as follows: $$\begin{array}{cc}\text{sin}\theta ={\displaystyle \frac{\text{opp}}{\text{hyp}}}\text{,}\hfill & \text{csc}\theta ={\displaystyle \frac{\text{hyp}}{\text{opp}}}\text{,}\hfill \\ \text{cos}\theta ={\displaystyle \frac{\text{adj}}{\text{hyp}}}\text{,}\hfill & \text{sec}\theta ={\displaystyle \frac{\text{hyp}}{\text{adj}}}\text{,}\hfill \\ \text{tan}\theta ={\displaystyle \frac{\text{opp}}{\text{adj}}}\text{,}\hfill & \text{cot}\theta ={\displaystyle \frac{\text{adj}}{\text{opp}}}\text{.}\hfill \end{array}$$	If $\text{cos}\alpha ={\displaystyle \frac{3}{8}}$ and $\alpha$ is an acute angle, find the other five trigonometric function values of 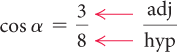$\alpha$. We find the missing length using the Pythagorean equation: $a^2+b^2=c^2$. $\begin{array}{c}\begin{array}{ccc}\hfill a^2+3^2& =\hfill & 8^2\hfill \end{array}\end{array}$