An Introduction to Optimization, 4th Edition

CHAPTER 16

SIMPLEX METHOD

16.1 Solving Linear Equations Using Row Operations

The examples in previous chapters illustrate that solving linear programs involves the solution of systems of linear simultaneous algebraic equations. In this section we describe a method for solving a system of n linear equations in n unknowns that we use in subsequent sections. The method uses elementary row operations and corresponding elementary matrices. For a discussion of numerical issues involved in solving a system of simultaneous linear algebraic equations, we refer the reader to [41] and [53].

An elementary row operation on a given matrix is an algebraic manipulation of the matrix that corresponds to one of the following:

1. Interchanging any two rows of the matrix

2. Multiplying one of its rows by a real nonzero number

3. Adding a scalar multiple of one row to another row

An elementary row operation on a matrix is equivalent to premultiplying the matrix by a corresponding elementary matrix, which we define next.

Definition 16.1 We call E an elementary matrix of the first kind if E is obtained from the identity matrix I by interchanging any two of its rows.

An elementary matrix of the first kind formed from I by interchanging the ith and the jth rows has the form

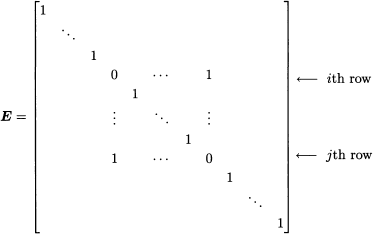
Note that E is invertible and E = E⁻¹.

Definition 16.2 We call E an elementary matrix of the second kind if E is obtained from the ...