An Introduction to Probability and Statistics, 3rd Edition

3MOMENTS AND GENERATING FUNCTIONS

3.1 INTRODUCTION

The study of probability distributions of a random variable is essentially the study of some numerical characteristics associated with them. These so-called parameters of the distribution play a key role in mathematical statistics. In Section 3.2 we introduce some of these parameters, namely, moments and order parameters, and investigate their properties. In Section 3.3 the idea of generating functions is introduced. In particular, we study probability generating functions, moment generating functions, and characteristic functions. Section 3.4 deals with some moment inequalities.

3.2 MOMENTS OF A DISTRIBUTION FUNCTION

In this section we investigate some numerical characteristics, called parameters, associated with the distribution of an RV X. These parameters are (a) moments and their functions and (b) order parameters. We will concentrate mainly on moments and their properties.

Let X be a random variable of the discrete type with probability mass function p_k = P{X = x_k}, k = 1, 2, …. If

(1)

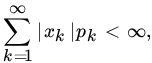
we say that the expected value (or the mean or the mathematical expectation) of X exists and write

(2)

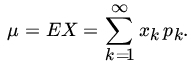
Note that the series may converge ...