Analysis of Complex Networks

14.6 Conclusion

The classification, developed here, is an extension of previous work of Deza and Shtogrin. It allows for various possible numbers of sides of interior faces and several possible holes. A natural question is if one can further enlarge the class of polycycles.

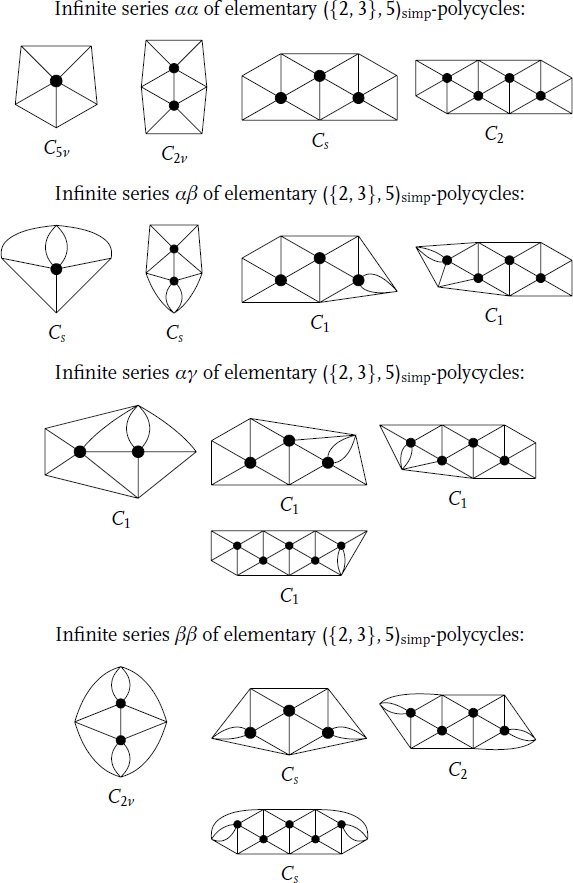
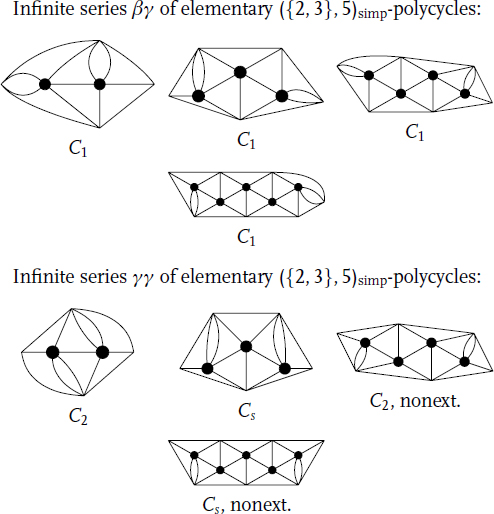
Figure 14.2 The first 4 members of the six infinite series of ({2, 3},5)_simp-polycycles from Theorem 14.5(iii).

There will be only some technical difficulties if one tries to obtain the catalog of elementary (R, Q)-polycycles, that is, the generalization of the (R, q) polycycle allowing the set Q for values of a degree of interior vertices. Such a polycycle is called an elliptic, a parabolic, or a hyperbolic if (where r = max_{i ∈R}ⁱ, q = max_{i ∈Q}ⁱ) is positive, zero, or negative, respectively. The decomposition and other main notions could be applied directly.

We required 2-connectivity and that any two holes not share a vertex. If one removes those two conditions, then too many other graphs appear.

The omitted cases (R, q) = ({2}, q) are not interesting. In fact, consider the infinite series of ({2}, 6)-polycycles, m-bracelets, m ≥ 2(i.e., m-circle with each edge being tripled). The central edge is a bridge for those ...