Analysis of Complex Networks

3.1 Introduction

The traditional manner in which information theory [1–3] is applied to characterize the structure and complexity of graphs [4–9] is based on the partitioning of a certain set of graph elements N (vertices, edges, two-edge subgraphs, etc.) into k equivalence classes, having a cardinality of N₁, N₂,..., N_k. This enables defining the probability of a randomly chosen element to belong to the class i as the ratio of the class cardinality and that of the entire set of graph elements, p_i = N_i/N. The Shannon equations for the mean and total information, Ī(α) and I(α),

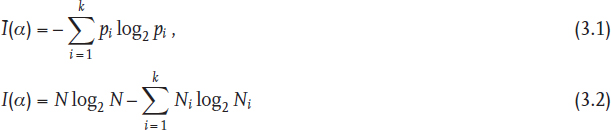
are then directly applicable.

Depending on the selected criterion of equivalence α, different classes and correspondingly different information measures can be ascribed to the graph. The simplest example is the partitioning of the graph vertices according to the vertex degree (the number of the nearest neighboring vertices), the first subset of vertices including those of degree 1, then those of degree 2, 3, etc. Accounting for the second, third, and so forth neighbors [10, 11] is another option, as is the most rigorous definition of vertex equivalence, the equivalence classes being the orbits of the automorphisms group of the graph. The symmetry operation in the latter case is the interchange of vertices without breaking any adjacency relationship [12].

While useful for a variety of applications, this manner ...