Analysis of Complex Networks

5.4 The Largest Component

In this section we assume α = 2, i.e., we work in binary n-cubes. All results and proofs easily extend to arbitrary alphabets. The analysis of large components presented here follows [20]. Section 5.3 has shown that the connectivity threshold reflects the disappearance of isolated vertices. Therefore, it seems natural to ask which probabilities we find a unique large component for. In addition, one would like to know its size. Note that the connectivity property alone is not sufficient for understanding the neutral evolution. The relevant property will be identified in Section 5.5 and is related to the emergence of short paths in n-cubes. Intuitively the largest component is in its “early” stage locally “treelike” and therefore not suited for preserving sequence-specific information. We set

and

We write a Qⁿ₂-vertex v=(x₁,...,x_n) as

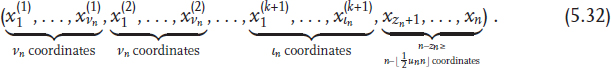
For any 1 ≤ s ≤ vⁿ, r = 1,..., k we set e(^r)_s to be the s+(r–1)v_n th-unit vector, i.e., e^(r) has exactly one 1 at its (s+(r–1)v_n)th coordinate. Similarly, let e^(k+1)(_s, 1 ≤ s ≤ l_n, denote the(s + kv_n)th-unit vector. We use the ...