Analysis of Financial Time Series, Third Edition

2.2 Correlation and Autocorrelation Function

The correlation coefficient between two random variables X and Y is defined as

where μx and μy are the mean of X and Y, respectively, and it is assumed that the variances exist. This coefficient measures the strength of linear dependence between X and Y, and it can be shown that − 1 ≤ ρx, y ≤ 1 and ρx, y = ρy, x. The two random variables are uncorrelated if ρx, y = 0. In addition, if both X and Y are normal random variables, then ρx, y = 0 if and only if X and Y are independent. When the sample is available, the correlation can be consistently estimated by its sample counterpart

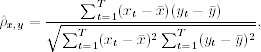
where and are the sample mean of X and Y, respectively.

Autocorrelation Function (ACF)

Consider a weakly stationary return series rt. When the linear dependence between rt and its past values rt−i is of interest, the concept of correlation is generalized to autocorrelation. The correlation coefficient between rt and rt−ℓ is called the lag-ℓ autocorrelation of rt