Chapter 5
System of Circles
5.1 RADICAL AXIS OF TWO CIRCLES
Definition 5.1.1: The radical axis of two circles is defined as the locus of a point such that the lengths of tangents from it to the two circles are equal.
Obtain the equation of the radical axis of the two circles S ≡ x2 + y2 + 2gx + 2fy + c = 0 and S1 ≡ x2 + y2 + 2g1x + 2fy + c1 = 0.
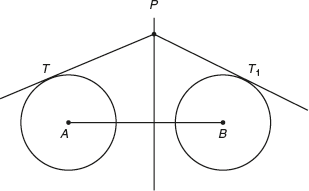
Let P(x1, y1) be a point such that the lengths of tangents to the two circles are equal.
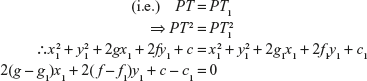
The locus of (x1, y1) is 2(g − g1)x + 2(f − f1)y + (c − c1) = 0 which is a straight line.
Therefore, the radical ...
Get Analytical Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

