
116 Applied calculus of variations for engineers
Γ
2
12
=
EG
u
− FE
v
2(EG − F
2
)
,
and
Γ
2
22
=
EG
v
− 2FF
v
+ FG
u
2(EG − F
2
)
.
These formulae all require that
EG − F
2
=0
which is true when a parameterization is regular.
8.2.1 Geodesics of surfaces of revolution
Another practically important special case is represented by surfaces of revo-
lution. Their generic description may be of the form
x = ucos(v),
y = usin(v),
and
z = f (u).
Here the last equation describes the meridian curve generating the surface.
The first order fundamental terms are
E =1+f
2
(u),
F =0,
and
G = u
2
.
The solution following the discussion in Section 8.1 becomes
v = c
1
1+f
2
(u)
u
u
2
− c
2
1
du + c
2
.
A simple sub-case of this class is a unit cylinder, described as
x = cos(v),
y = sin(v),
and
z = u.
The geometric meaning of the v parameter is the rotation angle generating
the cylinder’s circumference and the u parameter is the axial direction of the
Differential geometry 117
surface. The fundamental terms are
E =1,
F =0,
and
G =1.
The equation of the geodesic curve on the cylinder following above is
v = c
1
1
1
1 − c
2
1
du + c
2
,
or
v = c
1
1
1 − c
2
1
du + c
2
.
With
c
3
= c
1
1
1 − c
2
1
and integration we obtain
v = c
3
u + c
2
.
In the general case, this is a helix on the surface of the cylinder going through
the two points. This is also a line in the parametric space. This fact is geo-
metrically easy to explain because the cylinder is a developable surface. Such
a surface may be rectified onto a plane. In such a case the geodesic curve is
a straight line on the rectifying plane. The only curvature of the helix will be
that of the cylinder.
The constants of integration may be determined from the boundary condi-
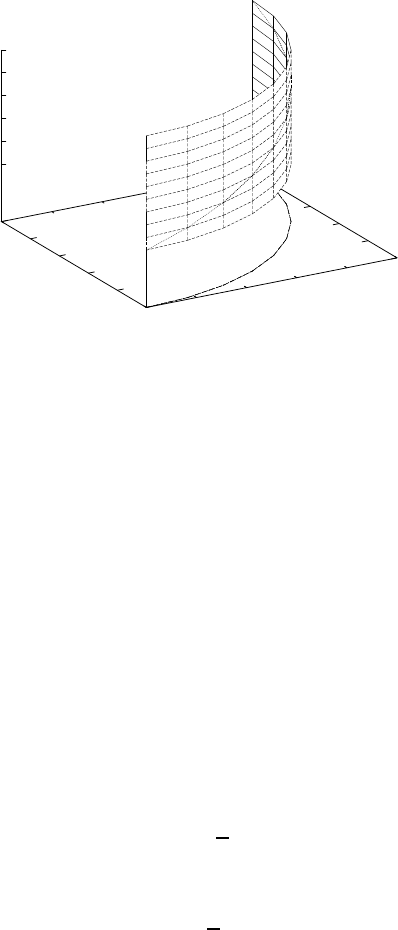
tions. For example, assume the case shown in Figure 8.1, where the starting
point is at
P
0
=(x
0
,y
0
,z
0
)=(1, 0, 0)
corresponding to parametric coordinates
u(t
0
)=0,v(t
0
)=0.
The endpoint is located at
P
1
=(x
1
,y
1
,z
1
)=(0, 1, 1)
corresponding to parametric coordinates
u(t
1
)=1,v(t
1
)=π/2.
118 Applied calculus of variations for engineers
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
FIGURE 8.1 Geodesic curve of a cylinder
Substituting the starting point yields
0=c
3
· 0+c
2
,
which results in
c
2
=0.
The endpoint substitution produces
π/2=c
3
· 1+c
2
,
andinturn
c
3
=
π
2
.
The specific solution for this case in the parametric space is
v =
π
2
u.
The Cartesian solution is obtained in the form of
x = cos(v),

Differential geometry 119
y = sin(v),
and
z =
v
π/2
.
It is easy to see that the latter equation makes the elevation change from zero
to 1, in accordance with the turning of the helix.
Since the parametric space of the cylinder is simply the rectangle of the
developed surface, it is easy to see some special sub-cases. If the two points
are located at the same rotational position (v = constant), but at different
heights, the geodesic curve is a straight line. If the two points are on the same
height (u = constant), but at different rotational angles, the geodesic curve is
a circular arc.
The last two sections demonstrated the difficulties of finding the geodesic
curves even on regular surfaces like the sphere or the cylinder. On a general
three-dimensional surface these difficulties increase significantly and may ren-
der using the differential equation of the geodesic curve unfeasible.
8.3 Geodesic curvature
Let us consider the parametric curve
r
(t)=x(t)i + y(t)j + z(t)k
on the surface
S(u, v)=x(u, v)i
+ y(u, v)j + z(u, v)k.
Let n
denote the unit normal of the surface. The curvature vector of a three-
dimensional curve is defined as
k
=
dt
dt
= t
,
where t
is the tangent vector computed as
t
=
dr
dt
,
and also assumed to be a unit vector (a unit speed curve) for the simplicity
of the derivation. Then the unit bi-normal vector is
b
= n × t.
Get Applied Calculus of Variations for Engineers, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

