Applied Computational Fluid Dynamics Techniques: An Introduction Based on Finite Element Methods, 2nd Edition

4 APPROXIMATION THEORY

The ideas of approximation theory are at the root of any discretization scheme, be it finite difference, finite volume, finite element, spectral element or boundary element. Whenever a PDE is solved numerically, the exact solution is being approximated by some known set of functions. How this is accomplished is described in the next two chapters. The present chapter is devoted to the basic notions in approximation theory. Throughout the book the Einstein summation convention will be used. Every time an index appears twice in an equation, the summation over all possible values of the index is assumed.

4.1. The basic problem

Simply stated, the basic problem is the following.

Given a function u(x) in the domain Ω, approximate u(x) by known functions Nⁱ (x) and a set of free parameters a_i:

The situation has been sketched in Figure 4.1.

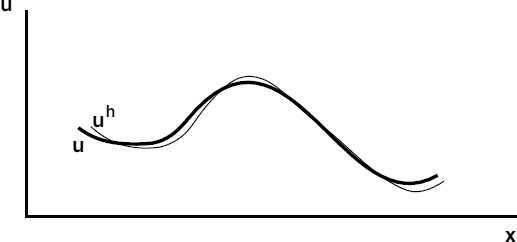
Figure 4.1. Approximation of functions

Examples of approximations that are often employed are:

• truncated Taylor series

  

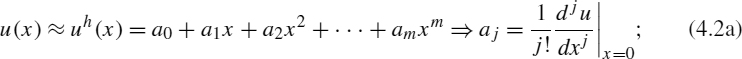
• Fourier expansions (e.g. truncated sine series)

  

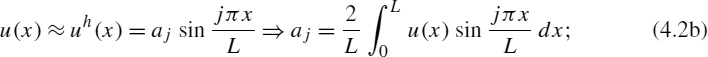
• Legendre polynomials;
• Hermite polynomials, etc.

In general, ...