10 EDGE-BASED COMPRESSIBLE FLOW SOLVERS
Consider the typical formation of a RHS using a finite element approximation with shape functions Ni. The resulting integrals to be evaluated are given by
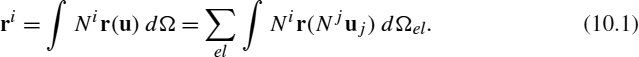
These integrals operate on two sets of data:
- (a) point data, for ri, ui; and
- (b) element data, for volumes, shape functions, etc.
The flow of information is as follows:
- GATHER point information into the element (e.g. ui );
- operate on element data to evaluate the integral in (10.1); and
- SCATTER-ADD element RHS data to point data to obtain ri.
For many simple flow solvers the effort in step 2 may be minor compared to the cost of indirect addressing operations in steps 1 and 3. A way to reduce the indirect addressing overhead for low-order elements is to change the element-based data structure to an edge-based data structure. This eliminates certain redundancies of information in the element-based data structure. To see this more clearly, consider the formation of the RHS for the Laplacian operator on a typical triangulation. Equation (10.1) may be recast as
![]()
This immediately opens three possibilities:
- obtain first the global matrix Kij and store it in some optimal way (using so-called sparse storage techniques);
- perform a loop over elements, obtaining rel and adding to r; and
- obtain ...
Get Applied Computational Fluid Dynamics Techniques: An Introduction Based on Finite Element Methods, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

