Applied Cryptography: Protocols, Algorithms, and Source Code in C, Second Edition

CHAPTER 23

Special Algorithms for Protocols

23.1 MULTIPLE-KEY PUBLIC-KEY CRYPTOGRAPHY

This is a generalization of RSA (see Section 19.3) [217,212]. The modulus, n, is the product of two primes, p and q. However, instead of choosing e and d such that ed ≡ 1 mod ((p - 1)(q - 1)), choose t keys, K_i, such that

Since

this is a multiple-key scheme as described in Section 3.5.

If, for example, there are five keys, a message encrypted with K₃ and K₅ can be decrypted with K₁, K₂, and K₄:

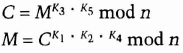
One use for this is multisignatures. Imagine a situation where both Alice and Bob have to sign a document for it to be valid. Use three keys: K₁, K₂, and K₃. The first two are issued one each to Alice and Bob, and the third is made public.

1. (1) First Alice signs M and sends it to Bob.

   

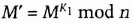
2. (2) Bob can recover M from M′.

   

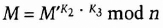
3. (3) He can also add his signature.

   

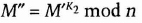
4. (4) Anyone can verify the signature with K₃, the public key. ...