Applied Digital Optics: From Micro-optics to Nanophotonics

Appendix B

The Scalar Theory of Diffraction

B.1 Full Scalar Theory

In order to introduce the concept of the scalar theory of diffraction, let us consider for a start an arbitrary wavefront U(x, y; z) propagating from z = 0 along the positive z-axis of a Cartesian referential [1]. The Fourier transform of such a wavefront is given by

The same arbitrary wavefront U(x, y; z) is thus the inverse Fourier transform of U(u, v; z), defined as

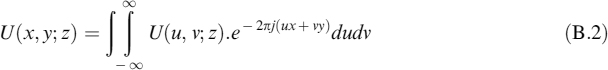
Therefore, U(x, y;z) can be described as an infinite composition of the set of functions e^{−2πj(ux + vy)} weighted by the coefficients of U(u, v; z). Bearing in mind the complex representation of plane waves (Equation (A.7)), it is obvious that these functions can be understood as sets of plane waves propagating in the z direction with the cosine direction

This means that U(x, y; z) can be decomposed into an angular spectrum of plane waves U(u, v; z). This angular spectrum of plane waves is also the Fourier transform of U(u, x; z), or the far-field representation of that same function.

Now let us examine how the angular spectrum propagates from a plane at z = 0 to a plane at z = z₀. We have therefore to find a relation between U(u, v; 0) and U(