4
INSTRUMENTAL VARIABLES
4.1 INTRODUCTION
The analysis methods presented in the previous chapters were based on the assumption that the independent variables are exogenous (E(ε|X) = 0). That is, the error terms in the linear regression model are uncorrelated or independent of the explanatory variables. In Chapter 1, we saw that under the exogeneity assumption, the least squares estimator b is an unbiased and consistent estimator of β. This chapter explores the properties of b under departures from the exogenous assumption? Explanatory variables that are not exogenous are called endogenous variables.
Under departures from the exogeneity conditions, b is no longer an unbiased and consistent estimator of β. To see this, in the simple linear regression case, consider the model yi = β0 + β1xi + εi where the disturbances are correlated with the explanatory variable. The least squares estimator of β1 is given by (Chapter 1)
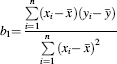
which upon simplifying can be written as
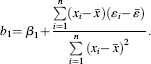
The second term gives the expression of the least squares estimator of a regression of ε on x. It should be obvious that the second term is not zero unless the disturbances are uncorrelated with the explanatory variable. Therefore, the least squares estimator of β1 is biased. The inconsistency of the least squares estimator can ...

