11
Householder Transformation and Tridiagonal Matrices
As in the last chapter, the focus of our discussion still continues to be the symmetric matrix. In this chapter, we study the Householder method to reduce a symmetric matrix to tridiagonal form. Next, we consider the problem of bracketing and determination of the eigenvalues of a symmetric tridiagonal matrix based on the Sturmian sequence property of its characteristic polynomial.
Householder Reflection Transformation
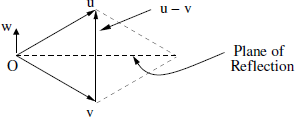
Figure 11.1: Vectors in Householder reflection
To appreciate the Householder reflection transformation, let us consider two vectors u, v ∈ Rk such that ∥u∥ = ∥v∥, as shown ...
Get Applied Mathematical Methods now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

