Applied Mathematics for Science and Engineering

4Numerical Quadrature

Introduction

Definite integrals must be evaluated routinely and for cases in which an antiderivative cannot be found, or for cases in which the analytic process is simply too difficult, a numerical scheme (numerical integration, or quadrature) may be our only recourse. Consider the integral

(4.1)

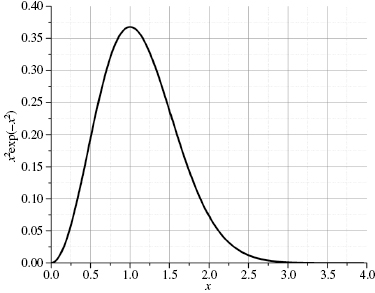
which we know to have the value . Let us consider a plot of the integrand as a function of x, shown in Figure 4.1.

Figure 4.1.  Behavior of x² exp(−x²). The value of the integral, eq. (4.1), is known to be .

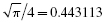We will conduct an elementary experiment with the graph of this integrand: First, we will count the smaller rectangular regions under the curve and add their areas together to obtain (70)(0.25)(0.025) = 0.4375. Next, we will cut out the region under the curve and weigh it and compare that weight to the average weight per rectangle. For the paper under the curve, we find W = 0.5754 g, and for each box, 0.008003 g. Therefore, the area under the curve is approximately 71.89 rectangular boxes or (71.89)(0.25)(0.025) = 0.4493. Our first estimate is in error by about 1.3% ...