Applied Mathematics for Science and Engineering

5Analytic Solution of Ordinary Differential Equations

An Introductory Example

Suppose we place about 500 mL of water in a beaker and heat the contents with a candle flame until the water begins to boil. We then remove the heat source and allow the contents of the beaker to cool simply by exposure to the ambient air. An approximate energy balance for this situation (the cooling process) can be written as

or symbolically as

(5.1)

In this first-order ordinary differential equation (ODE), m is the mass of heated water, C_p is the heat capacity of the water, h is the heat transfer coefficient, and A is the surface area for heat transfer. T_∞, of course, is the temperature of the air surrounding the beaker. Actual experimental data for this process are shown in Figure 5.1.

Figure 5.1.  Cooling process for 500 mL water, initially heated to incipient boiling. The heat source (flame) was removed at t = 865 s.

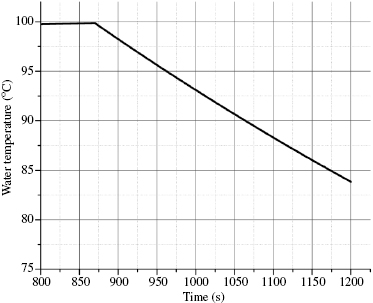
We want to solve eq. (5.1) and then see if the result is capable of describing the cooling process shown in Figure 5.1. It will be convenient to let θ = T − T_∞, such that

(5.2)

This equation ...