6Numerical Solution of Ordinary Differential Equations
An Illustrative Example
In engineering and the applied sciences, transient mass and energy balances arise frequently, often leading to ordinary differential equations (ODEs). Suppose, for example, we have a jacketed process vessel in which an exothermic chemical reaction may occur. The entering (feed) stream has a temperature, Tin; the well-mixed contents have temperature, T; and the steam used to heat the vessel has temperature, Ts. A verbal statement of the appropriate energy balance might appear:
And written out symbolically, we would expect something like this:
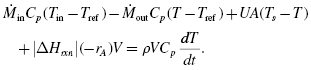
The rate at which the reactant species, A, is consumed is rA. We will let the mass flow rates in and out be the same, and we set the reference temperature equal to the inlet (feed) temperature and divide by ![]() :
:
Please note that every term in the equation has the dimension of temperature. The characteristic time, τ, that appears on the right-hand side is the total mass in the vessel divided by the mass flow rate, and it is the time constant for this system. ...
Get Applied Mathematics for Science and Engineering now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

