APPLIED MULTIVARIATE STATISTICS: WITH SAS® SOFTWARE

1.2. Random Vectors, Means, Variances, and Covariances

Suppose y1,...,y_p are p possibly correlated random variables with respective means (expected values) μ1, ..., μ_p. Let us arrange these random variables as a column vector denoted by y, that is, let

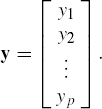
We do the same for μ₁, μ₂, ..., μ_p, and denote the corresponding vector by μ. Then we say that the vector y has the mean μ or in notation E(y) = μ.

Let us denote the covariance between y_i and y_j by σ_ij, i, j = 1, ..., p, that is

σ_ij = cov(y_i, y_j) = E[(y_i - μ_i)(y_j - μ_j)] = E[(y_i - μ_i)y_j] = E(y_iy_j) - μ_iμ_j

and let

Since cov(y_i, y_j) = cov(y_j, y_i), we have σ_ij = σ_ij. Therefore, Σ is symmetric with ...