Arithmetic and Logic in Computer Systems

8

Floating Point Operations

Floating point operations are widely applied in scientific computations. With limited number of digits, the range and precision of the numbers represented by floating point systems can be improved. In this chapter, we introduce floating point addition, subtraction, multiplication and division.

8.1 FLOATING POINT ADDITION/SUBTRACTION

Let X₁ = (M₁, E₁) and X₂ = (M₂, E₂) be two numbers in floating point representation, where M_i = S_i|M_i| and X_i = (−1)^S_i · |M_i| · r^E_i−bias. We are to find X_out = X₁ ± X₂.

Two floating point numbers cannot be added/subtracted unless the two exponents of them are equal. An alignment is needed if the exponents of the two given numbers are different. Usually, we let the bigger exponent remain unchanged, and adjust the smaller exponent to be the same as the bigger one. For a number with exponent enlarged, its mantissa should be reduced in order to keep the value of the number as same as before. That is, the mantissa should be shifted right. The exponent was increased by |E₁ − E₂|, resulting in r^{|E₁−E₂|} times enlargement. The number of digit positions to be right shifted in mantissa should be |E₁ − E₂| as well resulting in r^{|E₁−E₂|} times reduction (indicated by a factor of r^{−(|E₁−E₂|)} below).

Let X_out = X₁ ± X₂ = (M_out, E_out). We have

E_out = max{E₁, E₂},

and

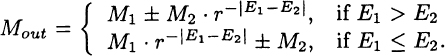
The addition/subtraction procedure includes the following steps.

1. Alignment. ...