Automation for Robotics

1

Modeling

We will call modeling the step that consists of finding a more or less accurate state representation of the system we are looking at. In general, constant parameters appear in the state equations (such as the mass or the inertial moment of a body, the coefficient of viscous friction, the capacitance of a capacitor, etc.). In these cases, an identification step may prove to be necessary. In this book, we will assume that all the parameters are known, otherwise we invite the reader to consult Eric Walter’s book [WAL 14] for a broad range of identification methods. Of course, no systematic methodology exists that can be used to model a system. The goal of this chapter and of the following exercises is to present, using several varied examples, how to obtain a state representation.

1.1. Linear systems

In the continuous-time case, linear systems can be described by the following state equations:

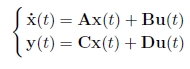
Linear systems are rather rare in nature. However, they are relatively easy to manipulate using linear algebra techniques and often approximate in an acceptable manner the nonlinear systems around their operating point.

1.2. Mechanical systems

The fundamental principle of dynamics allows us to easily find the state equations of mechanical systems (such as robots). The resulting calculations are relatively complicated for complex systems and the use of computer algebra systems may prove to ...