Automation for Robotics

4

Linear Control

In this chapter, we will study the design of controllers for systems given by linear state equations of the form:

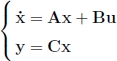
We will show in the following chapter that around very particular points of the state space, called operating points, many nonlinear systems genuinely behave like linear systems. The techniques developed in this chapter will then be used for the control of nonlinear systems. Let us denote by m, n, p the respective dimensions of the vectors u, x and y. Recall that A is called evolution matrix, B is the control matrix and C is the observation matrix. We have assumed here, in the interest of simplification, that the direct matrix D involved in the observation equation was nil. In the case where such a direct matrix exists, we can remove it with a simple loop as shown in Exercise 4.1.

After having defined the fundamental concepts of controllability and observability, we will propose two approaches for the design of controllers. First of all, we will assume that the state x is accessible on demand. Even though this hypothesis is generally not verified, it will allow us to establish the principles of the pole placement method. In the second phase, we will no longer assume that the state is accessible. We will then have to develop state estimators capable of approximating the state vector in order to be able to employ the tools developed in the first phase. The ...