Automation for Robotics

5

Linearized Control

In Chapter 4, we have shown how to design controllers for linear systems. However, in practice, the systems are rarely linear. Nevertheless, if their state vector remains localized in a small zone of the state space, the system may be considered linear and the techniques developed in Chapter 4 can then be used. We will first show how to linearize a nonlinear system around a given point of the state space. We will then discuss how to stabilize these nonlinear systems.

5.1. Linearization

5.1.1. Linearization of a function

Let f: be a differentiable function. In the neighborhood of a point , the first-order Taylor development of f around gives us:

with:

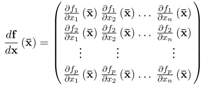
This matrix is called the Jacobian matrix. Very often, in order to linearize a function, we use formal calculus for calculating the Jacobian matrix, then we instantiate this matrix around . When we differentiate by hand, we avoid ...