18.1 Tracking a Target in Cartesian Coordinates
In this section, we discuss methods of tracking an object when our tracking filter uses a state vector that is defined in Cartesian coordinates. The section is divided into subsections where we discuss the dynamic model used to define the expected object motion (Section 18.1.1), the observation vector and how it is related to the state vector (Section 18.1.2), and the various Cartesian Gaussian filter tracking algorithms that can applied to this problem (Section 18.1.3). A discussion of filter initialization and the creation of a Monte Carlo set of observations will be delayed until Sections 18.3.
18.1.1 Object Dynamic Motion Model
The standard method for tracking a moving object from a set of stationary radars in Cartesian coordinates assumes that the object travels at a constant velocity. This results in a linear dynamic model of the form
where the Cartesian state vector at time tn is defined by
(18.2) ![]()
and the transition matrix Fn is defined as
(18.3) 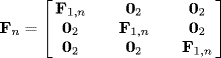
with
(18.4) ![]()
02 a 2 × 2 matrix of zeros and Tn is defined as
(18.5)
Note that ...
Get Bayesian Estimation and Tracking: A Practical Guide now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

