Bayesian Estimation and Tracking: A Practical Guide

Appendix 19.A quaternions, Axis-Angle Vectors, and Rotations

19.A.1 Conversions Between Rotation Representations

Let be used as an axis-angle representation of rotation where the direction of a specifies the axis of rotation and specifies the magnitude of rotation (in radians).

Let , where H is the space of quaternions, be used as a unit quaternion representation of rotation, where q_s is real and q_x, q_y,q_z are coefficients of distinct imaginary numbers, and .

Let be a 3 × 3 rotation matrix, such that M is orthonormal, and det M = + 1.

To convert from an axis-angle vector a to a unit quaternion q, we define the function as

(19.161)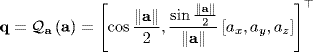

To convert from a unit quaternion q to an axis-angle vector a we define the function as

(19.162)

To convert from a unit quaternion q to a rotation matrix