Beginning Partial Differential Equations, 3rd Edition

Chapter 8

First-Order Equations

Up to this point we have concentrated on problems involving second-order partial differential equations. These see wide application and also have a rich theory that leads naturally to further topics in partial differential equations.

Higher order differential equations occur, for example, in modeling buckling of beams in elasticity theory. In the other direction, first-order equations are also seen in many contexts. As an illustration, we will derive an equation known as a conservation law.

Imagine a fluid, or perhaps energy, flowing in some medium. As a ” “thought device” constructed to analyze the flow, imagine a channel or tube in the medium, aligned along an x–axis, with uniform cross sections of area A (Figure 8.1). The fluid flows from left to right in the diagram.

Figure 8.1: Derivation of a conservation law.

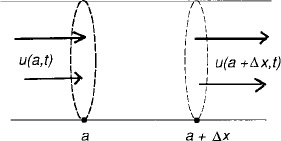
Let u(x, t) be the fluid density (amount per unit volume) at time t and point x. Choose any point a and any Δx > 0 and consider the segment of tube between a and a + Δx. The fluid is flowing into this segment over the cross section at a and out through the cross section at a + Δx. Let φ(x, t) be the flux of the fluid at time t, so Aφ(x, t) is the quantity flowing across the section at x, at time t. Finally, let S(x, t) account for sources or sinks (fluid being produced or lost, per unit area of the cross section at x at time t). We want ...