where ![]() is the encoder state after the encoding of bit
is the encoder state after the encoding of bit ![]() .
.
The LLR of bit ![]() can then be expressed as
can then be expressed as
(12)
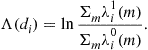 (12)
(12)
For the code of Figure 26, is written as
Get Channel Coding: Theory, Algorithms, and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

