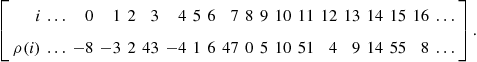5.4.2 Implementation of convolutional interleavers with minimal memory requirement
We have ...
Get Channel Coding: Theory, Algorithms, and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.