Circuit Oriented Electromagnetic Modeling Using the PEEC Techniques

Chapter 4Capacitance Computations

We consider capacitance modeling in this chapter. Capacitance calculations have a long history from Maxwell [1] to early precomputer work, for example, Ref. [2]. However, the majority of the important work is based on the availability of computers, for example, Refs [3–5].

Capacitance computations also represent a key component of partial element equivalent circuit (PEEC) models. This is evident from Chapter 6. Subdividing the conductors into cells is fundamental to PEEC. Two different issues exist. As shown in Fig. 4.1, the charge on the conductors is not uniform. However, the potential of a conducting plate is constant as shown. As we will see, at high frequencies conducting surfaces are no longer equipotentials. In both cases, we need to subdivide the plate into cells such that the charge can assume a different value at each cell.

We start out with the computation of capacitance as a stand-alone solution. This expands the scope of this chapter and it includes aspects that are important for capacitance modeling in general. We hope that this gives the reader a good understanding on how to compute and approximate capacitance values.

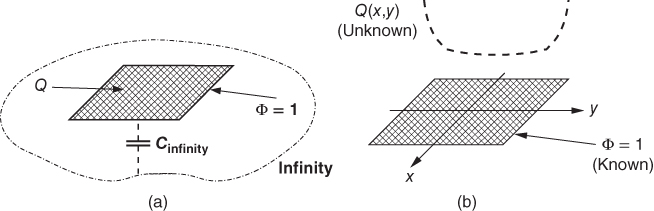
Figure 4.1 Single plate. (a) Capacitance to infinity. (b) Charge distribution.

To start with, we assume that we want to compute the capacitance for a thin conducting plate or a set of plates. For the single plate, ...