Problem 2
Galileo and a Discovery Concerning Dice (1620)
Problem. Suppose three dice are thrown and the three numbers obtained added. The total scores of 9, 10, 11, and 12 can all be obtained in six different combinations. Why then is a total score of 10 or 11 more likely than a total score of 9 or 12?
Solution. Table 2.1 shows each of the six possible combinations (unordered arrangements) for the scores of 9–12. Also shown is the number of ways (permutations or ordered arrangements) in which each combination can occur.
Table 2.1 Combinations and Number of Ways Scores of 9–12 that Can Be Obtained When Three Dice are Thrown.
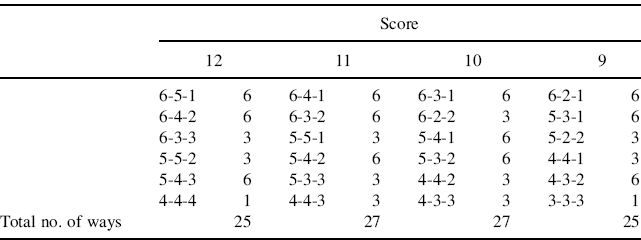
For example, reading the first entry under the column 12, we have a 6-5-1. This means that, to get a total score of 12, one could get a 6, 5, 1 in any order. Next to the 6-5-1 is the number 6. This is the number of different orders in which one can obtain a 6, 5, 1. Hence, we see that the scores of 9–12 can all be obtained using six combinations for each. However, because different combinations can be realized in a different number of ways, the total number of ways for the scores 9, 10, 11, and 12 are 25, 27, 27, and 25, respectively. Hence, scores of 10 or 11 are more likely than scores of 9 or 12.
2.1 Discussion
Almost a century after Cardano's times, this problem was asked by the Grand Duke of Tuscany to the renowned physicist and mathematician Galileo Galilei ...

