Problem 3
The Chevalier de Méré Problem I: The Problem of Dice (1654)
Problem. When a die is thrown four times, the probability of obtaining at least one six is a little more than 1/2. However, when two dice are thrown 24 times, the probability of getting at least one double-six is a little less than 1/2. Why are the two probabilities not the same, given the fact that Pr{double-six for a pair of dice} = 1/36 =1/6·Pr{a six for a single die}, and you compensate for the factor of 1/6 by throwing 6 · 4 = 24 times when using two dice?
Solution. Both probabilities can be calculated by using the multiplication rule of probability. In the first case, the probability of no six in one throw is 1 − 1/6 = 5/6. Therefore, assuming independence between the throws,
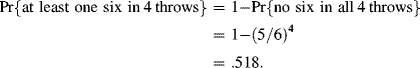
In the second case, the probability of no double-six in one throw of two dice is 1 − (1/6)2 = 35/36. Therefore, again assuming independence,
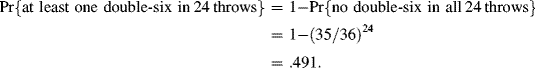
3.1 Discussion
It is fairly common knowledge that the gambler Antoine Gombaud (1607–1684), better known as the Chevalier de Méré,1 had been winning consistently by betting even money that a six would come up at least once in four rolls with a single die. However, he had now been losing other bets, when in 1654 he met his friend, the amateur mathematician Pierre de Carcavi (1600–1684). This was ...

