Problem 10
De Moivre, Gauss, and the Normal Curve (1730, 1809)
Problem. Consider the binomial expansion of 
, where n is even and large. Let M be the middle term and Q be the term at a distance d from M. Show that
(10.1) 
Solution. We let 
, where m is a positive integer. Then
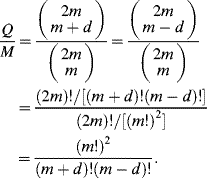
Applying Stirling's formula 
for large N, we have
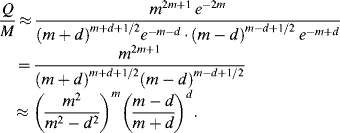
Taking logarithms on both sides, with d/m small, we have
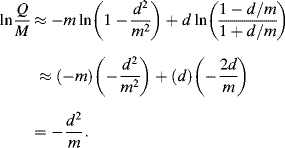
Writing 
, we have 
, as required.
10.1 Discussion
The above result was first obtained by Abraham de Moivre (1667–1754) (Fig. 10.3) in an attempt to approximate the symmetric binomial distribution. De Moivre started this ...
