Classic Problems of Probability

Problem 14

Bayes, Laplace, and Philosophies of Probability (1764, 1774)

Problem. Assume that the probability p of an event A is equally likely to be any number between 0 and 1. Show that, conditional on A having previously occurred in a out of n independent and identical trials, the probability that p lies between p₁ and p₂ is

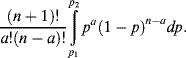
Solution. Let X_n be the number of times that the event A occurs in n trials. Since p is equally likely to be between 0 and 1, we let p have a probability density function that is uniform on [0,1], that is,

To find , let us first obtain the conditional density by using Bayes' Theorem¹:

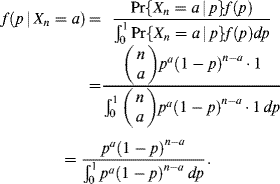
Now, we have²

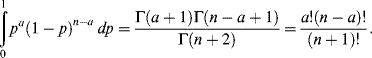
Therefore,

Hence,

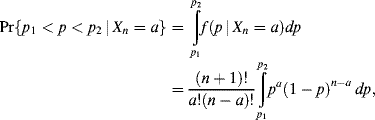
as required.

14.1 Discussion

This is essentially ...