Classic Problems of Probability

Problem 18

Bertrand's Strange Three Boxes (1889)

Problem. There are three boxes, each with two drawers. Box A contains one gold coin in each drawer, box B contains one silver coin in each drawer, and box C contains one gold coin in one drawer and one silver coin in the other.

a. A box is chosen at random. What is the probability that it is box C?

b. A box is chosen at random and a drawer opened at random. The coin is removed. Suppose it is a gold coin. What is the probability that the box chosen is box C?

Solution. (a) All three boxes have the same chance of being chosen. So, the probability that box C is chosen is 1/3.

(b) Let C be the event “box C is chosen”, and similarly for events A and B. Let G be the event “a gold coin is found in one of the drawers from the chosen box”. Then

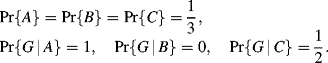
Using Bayes' Theorem,⁴ we have

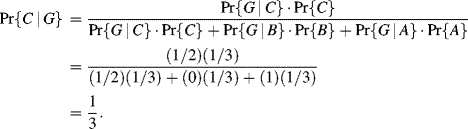
18.1 Discussion

Although the name of Joseph Louis François Bertrand (1822–1900) is usually associated with the chord paradox (see Problem 19), his treatise Calculs des Probabilités¹ (Bertrand, 1889) is a treasure-trove of several interesting probability problems. Of these, the box problem appears as the second problem in the book.² However, the second part of the original question is in a slightly different form from that presented in (b) in the Problem. On p. 2 of his ...