Classic Problems of Probability

Problem 24

Of Borel, Monkeys, and the New Creationism (1913)

Problem. A robot monkey is seated at a typewriter and randomly hits the keys in an infinite sequence of independent trials. Prove that, theoretically, the monkey will eventually type out the complete works of Shakespeare with certainty.

Solution. Let the number of keys on the keyboard be K, and the complete works of Shakespeare form a sequence of S letters, where both K and S are finite numbers. Divide the sequence of letters typed by the monkey into segments Seg₁, Seg₂, . . ., each S letters long. Now, the probability that the ith letter typed by the monkey coincides with the ith letter in the works of Shakespeare is 1/K. Thus, the probability that segment Seg₁ corresponds to the sequence in the works of Shakespeare, that is, the probability that Seg₁ is a “success” is . Next consider the first G segments typed by the monkey. The probability that every one of the G segments is a “failure” . Therefore, the probability that at least one of the G segments is a “success” is

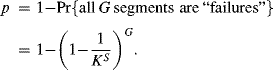
Since the robot monkey types an infinite number of letters, we have

Now, is a real number in (0, 1) so that

and

Hence, theoretically, the monkey will ...