Classical Geometry: Euclidean, Transformational, Inversive, and Projective

CHAPTER 1

CONGRUENCY

1.1 Introduction

Assumed Knowledge

This text assumes a bit of knowledge on the part of the reader. For example, it assumes that you know that the sum of the angles of a triangle in the plane is 180° (x + y + z = 180° in the figure below), and that in a right triangle with hypotenuse c and sides a and b, the Pythagorean relation holds: c² = a² + b².

We use the word line to mean straight line, and we assume that you know that two lines either do not intersect, intersect at exactly one point, or completely coincide. Two lines that do not intersect are said to be parallel.

We also assume certain knowledge about parallel lines, namely, that you have seen some form of the parallel axiom:

Given a line l and a point P in the plane, there is exactly one line through P parallel to l.

The preceding version of the parallel axiom is often called Playfair’s Axiom. You may even know something equivalent to it that is close to the original version of the parallel postulate:

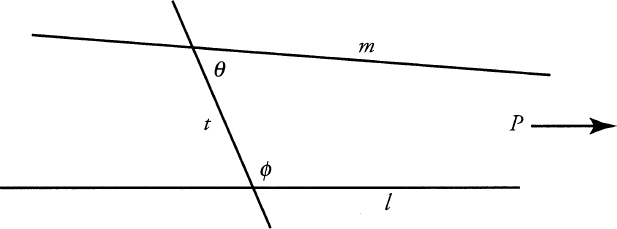
Given two lines l and m, and a third line t cutting both l and m and forming angles ϕ and θ on the same side of t, if ϕ + θ < 180°, then l and m meet at a point on the same side oft as the angles.