CHAPTER 7
THE EUCLIDEAN TRANSFORMATIONS OR ISOMETRIES
7.1 Rotations, Reflections, and Translations
Two children want to share a piece of cake of an unusual shape, as shown in the figure on the following page, where BCDE is a square, the curve AE is a circular arc with center C, and the points A, B, and E are collinear. Being children, they are not enthusiastic about receiving pieces that differ in shape. In other words, they want to cut the cake into two congruent pieces. How can this be done?

If the cake included the square space above BCDE, so that it was of the shape shown in the figure on the right, the task would be very simple. The cake could be cut down the middle along the line l.
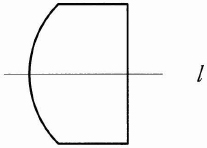
The cake in this figure has reflectional symmetry about the line l: if you hold a mirror vertical to the page with one edge of the mirror along l, the reflection of one half of the figure will coincide with the other half (this type of symmetry will be defined more precisely later).
When we wish to divide cakes and pies equally, we tend to look for reflectional symmetry and often overlook other possibilities. This might be why many people try to divide the cake by cutting it into two pieces and then dividing each of the pieces along an axis of reflectional symmetry, as in the figure on the right. ...
Get Classical Geometry: Euclidean, Transformational, Inversive, and Projective now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

