Classical Geometry: Euclidean, Transformational, Inversive, and Projective

CHAPTER 9

THE PRODUCT OF DIRECT ISOMETRIES

Given two direct isometries, say the rotation R_P,ϕ and the translation T_AB, we know that their product R_P,ϕ T_AB is a direct isometry, and we may even suspect that it is a rotation R_Q,θ. The question is, what is Q and what is θ? This chapter will describe some of the ways that we can determine the values of the parameters that describe the result, in this case, Q and θ.

9.1 Angles

We first need to clear up some possible ambiguities about directed angles.

In Example 8.3.2, we showed that the product of two reflections in nonparallel lines is a rotation whose center is the intersection point of the two lines and whose angle of rotation is twice the angle from the first line to the second line; that is,

where Q = l ∩ m and where α is twice the directed angle from l to m. If l and m are rays, as in (a) below, there is no ambiguity in the meaning of the phrase “the directed angle from l to m.” We can think of it as being 36° or −324°, since we identify the angles of θ and θ + 360n for all integers n.⁸

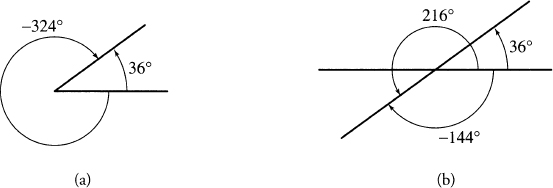
When we talk about the directed angle from one line to another, however, there are other possible interpretations. In (b) above, in addition to 36° and −324°, the directed angle from l to m can be legitimately interpreted as 216° or −144°. Does ...