CHAPTER 14
RECIPROCATION AND THE EXTENDED PLANE
14.1 Harmonic Conjugates
If A and B are two points on a line, any pair of points C and D on the line for which
![]()
is said to divide AB harmonically. The points C and D are then said to be harmonic conjugates with respect to A and B.
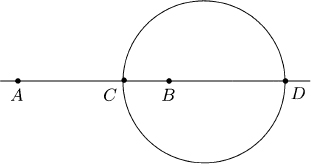
Lemma 14.1.1. Given ordinary points A and B, and given a positive integer k where k ≠ 1, there are two ordinary points C and D such that
![]()
One of the points C and D is between A and B, while the other is exterior to the segment AB.
Proof. Choose a point C on the line AB such that
![]()
Since k > 0, then CB < AB, and we may assume that C lies between A and B.
Now, we have
![]()
so that
![]()
that is,
![]()
Now we find the point D, which will be exterior to the segment AB—beyond B if k > 1 and beyond A if 0 < k < 1.
Assuming that k > 1, ...
Get Classical Geometry: Euclidean, Transformational, Inversive, and Projective now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

