5 COMBINING CONTINUOUS-VALUED OUTPUTS
5.1 DECISION PROFILE
Consider the canonical model of a classifier illustrated in Figure 1.9. The degrees of support for a given input x can be interpreted in different ways, the two most common being confidences in the suggested labels and estimates of the posterior probabilities for the classes.
Let ![]() be a feature vector and Ω = {ω1, ω2, …, ωc} be the set of class labels. Each classifier Di in the ensemble
be a feature vector and Ω = {ω1, ω2, …, ωc} be the set of class labels. Each classifier Di in the ensemble ![]() outputs c degrees of support. Without loss of generality we can assume that all c degrees are in the interval [0, 1], that is,
outputs c degrees of support. Without loss of generality we can assume that all c degrees are in the interval [0, 1], that is, ![]() . Denote by di, j(x) the support that classifier Di gives to the hypothesis that x comes from class ωj. The larger the support, the more likely the class label ωj. The L classifier outputs for a particular input x can be organized in a decision profile (DP(x)) as the matrix shown in
Figure 5.1.
. Denote by di, j(x) the support that classifier Di gives to the hypothesis that x comes from class ωj. The larger the support, the more likely the class label ωj. The L classifier outputs for a particular input x can be organized in a decision profile (DP(x)) as the matrix shown in
Figure 5.1.
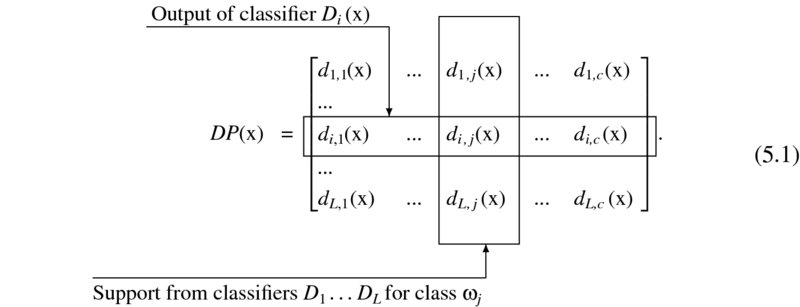
FIGURE 5.1 Decision profile for an input x.
The methods described in this chapter use DP(x) to find the overall support for each class, and subsequently label the input x in the class with the largest support. There are two ...
Get Combining Pattern Classifiers: Methods and Algorithms, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

