Common Errors in Statistics (and How to Avoid Them), 4th Edition

COMPARING THE MEANS OF K SAMPLES

Although the traditional one-way analysis of variance based on the F-ratio

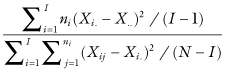
is highly robust, it has four major limitations:

1. Its significance level is dependent on the assumption of normality. Problems occur when data are drawn from distributions that are highly skewed or heavy in the tails. Still, the F-ratio test is remarkably robust to minor deviations from normality.

2. Not surprisingly, lack of normality also affects the power of the test, rendering it suboptimal.

3. The F-ratio is optimal for losses that are proportional to the square of the error and is suboptimal otherwise.

4. The F-ratio is an omnibus statistic offering all-round power against many alternatives but no particular advantage against any specific one of them. For example, it is suboptimal for testing against an ordered dose response when a test based on the correlation would be preferable.

A permutation test is preferred for the k-sample analysis [Good and Lunneborg, 2005]. These tests are distribution free (though the variances must be the same for all treatments). They are at least as powerful as the analysis of variance. And you can choose the test statistic that is optimal for a given alternative and loss function and not be limited by the availability of tables.

We take as our model X_ij = α_i + ε_jj, where i = 1, … I denotes the treatment, and j = 1, … , n_i . We assume ...