Competing with High Quality Data: Concepts, Tools, and Techniques for Building a Successful Approach to Data Quality

Appendix B

Matrix Theory: Related Topics

What Is a Matrix?

A matrix is an array of elements arranged in rows and columns. Matrix manipulations play a significant role in multivariate analysis, or pattern analysis.

If matrix A has m rows and n columns, then we say that matrix A is of size m × n. An example of 3 × 4 matrix is shown as follows:

Transpose of a Matrix

If the rows and columns of matrix A are interchanged, the resultant matrix is called the transpose of matrix A and is denoted by A^T or A′. If A is of size m × n, then A^T is of size n × m. The transpose of A is a 3 × 4 matrix and is shown as follows:

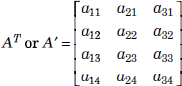
Square Matrix

If the number of rows and the number of columns of a matrix are the same, then that matrix is called a square matrix.

Determinant of a Matrix

The determinant is a characteristic number associated with a square matrix. The importance of the determinant can be realized when solving a system of linear equations using matrix algebra. The solution to the system of equations contains the inverse matrix term, which is obtained by dividing the adjoint matrix by the determinant. If the determinant is zero, then the solution does not exist.

Let us consider a 2 × 2 matrix, as follows:

The determinant of this matrix is a₁₁a₂₂ − a₁₂a₂₁.

Now let us consider a 3 × 3 ...